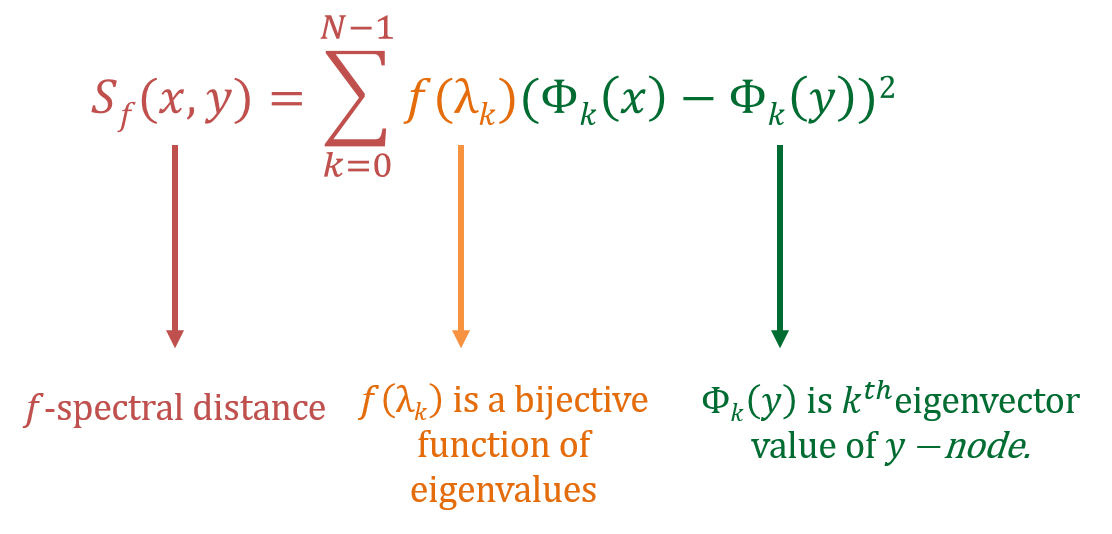Blog: Machine Learning Equations by Saurabh Verma

Graph is a fundamental but complicated structure to work with from machine learning point of view. Think about it, a machine learning model usually require inputs in some form of mathematical objects like vectors, matrices, real number sequences and then produces the desired outputs. So, the question is how we can convert a graph into a mathematical object that is suitable for performing machine learning tasks such as classification or regression on graphs.

For past one year, I have been working on developing machine learning models for graph(s) in order to solve two specific problems:

1) Graph Classification: Given a collection of graphs $\{G_i\}_{i=1}^{M}$ and associated graph labels $\{y_i\}_{i=1}^{M}$ where $y_i\in \mathbf{R^{c}}$ ($c$ is the number of classes), we need to come up with a learning model or function $F:G \rightarrow Y$ that can classify or predict the label associated with a graph.

2) Node Classification: Given a graph $G=(V,E,W)$, where $V$ is vertex set, $E$ is edge set & $W$ is adjacency matrix and labels $\{y_i\}_{i=1}^{M}$ where $y_i\in \mathbf{R^{c}}$ associated with each node, our task is to classify or predict the labels on each node. That is, come up a learning function $F:V\rightarrow Y$.

In this blog, I’ll mainly focus on graph classification problem but also show how we can leverage this work to perform node label classification as well. The fundamental problem in graph classification is comparing two graph structures. The main hurdle in comparing two graph structures is that we don’t know which node in the first graph corresponds to which node in other graph. This problem is universally known as graph isomorphism problem and so far we know it can only be solved in quasi-polynomial time and that too theoretically. Hence people came up with approximate but polynomial alternatives.

Previous studies on graph classification can be grouped into three main categories.
1) Graph Spectrum 2) Graph Kernels 3) Graph Convolutional Networks.

Graph Spectrum: Our majority work falls under first category and similar to graph kernels in certain aspects. But without going too much into $-$ what is graph kernel and graph convolutional network $-$ I’ll lay out the ideas behind graph spectrum.

First let’s discuss what spectrum mean? Spectrum is a collection of atomic elements (say in form of a set or vector or other mathematical object) to represent objects belonging to the same class (here class of objects could be an electrical signal, an audio signal or a chemical compound). For example, time series signal has a frequency spectrum. The importance of frequency spectrum is that one can recover the whole original signal from its frequency spectrum. Secondly from learning point of view, spectrum gives us a convenient and rich way to compare the similarity between two signals.

Now, the question is does graph has a spectrum? And if so, what are its atomic elements?

The most common graph spectrum you may heard of is graph Laplacian eigenvalue spectrum, where atomic elements are eigenvalues of graph Laplacian matrix. There are two more powerful graph spectrums based on group theory: Skew Spectrum and Graphlet Spectrum. The best thing about graph spectrum is that it atomic elements are solely depends upon the structure of the graph and thus invariant to permutation of graph vertex labels – a very important property desired from learning point of view.

We propose a new graph spectrum which is conceptually simple to understand but at the same time powerful enough as I’ll try to convince. Our Idea: Graph atomic structure (or spectrum) is encoded in the multiset of all nodes pairwise distances.

But what distance one should consider on a Graph?

$$\definecolor{color1}{RGB}{114,12,63} \color{color1} \text{Welcome to The Family of Graph Spectral Distances $({\rm F{\scriptsize GSD}})$ }$$

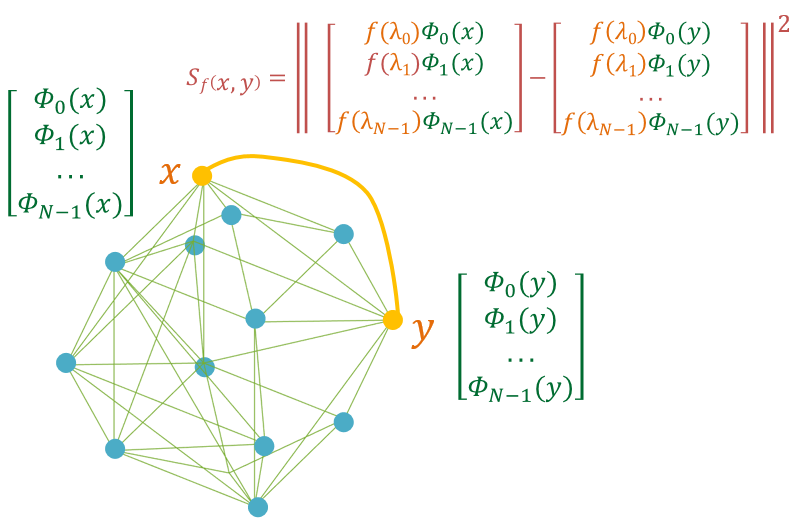
${\rm F{\scriptsize GSD}}$ is based on graph Laplacian $(L=D-W)$ spectral properties. Here $\phi_{k}$ & $\lambda_k$ is $k^{th}$ Laplacian eigenvector and eigenvalue respectively.

So what’s special about this family of distance? Depending upon $f(\lambda)$, ${\rm F{\scriptsize GSD}}$ can capture different type of information about graph sub-structures.

${\rm F{\scriptsize GSD}}$ Elements Encode Local Structure Information: For $f(\lambda)=\lambda^p$ ($p\geq 1$), one can show that $\mathcal{S}_f(x,y)$ takes only $p$-hop local neighborhood information.
${\rm F{\scriptsize GSD}}$ Elements Encode Global Structure Information: For $f(\lambda)=\frac{1}{\lambda^p}$ ($p\geq 1$), one can show that $\mathcal{S}_f(x,y)$ captures global structure information.

Some Known Graph Distances Can Be Derived From ${\rm F{\scriptsize GSD}}$.

• Setting $f(\lambda)=\frac{1}{\lambda}$ yields is harmonic or effective resistance distance.
• Setting $f(\lambda)=\frac{1}{\lambda^2}$ yields biharmonic distance.
• Setting $f(\lambda)=e^{-2 \lambda}$ yields heat diffusion distance.

Theorem 1 (Uniqueness of ${\rm F{\scriptsize GSD}}$): The $f$-spectral distance matrix $\mathcal{S}_f=[ \mathcal{S}_f(x,y)]$ uniquely determines the underlying graph (up to graph isomorphism), and each graph has a unique $\mathcal{S}_f$ (up to permutation). More precisely, two undirected, weighted (and connected) graphs $G_1$ and $G_2$ have the same ${\rm F{\scriptsize GSD}}$ based distance matrix up to permutation, i.e., $\mathcal{S}_{G_1}=P\mathcal{S}_{G_2}P^{T}$ for some permutation matrix $P$, if and only if the two graphs are isomorphic.

Implications: One of the consequence of Theorem $1$ is that the $\mathcal{R}$ based on multiset of ${\rm F{\scriptsize GSD}}$ is invariant under the permutation of graph vertex labels. Unfortunately, it is possible that the multiset of some ${\rm F{\scriptsize GSD}}$ members can be same for non-isomorphic graphs (otherwise, we would have a $\mathcal{O}(N^2)$ polynomial time algorithm for solving graph isomorphism problem!). However, there is lot of HOPE. It is known that all non-isomorphic graphs with less than nine vertices have unique multisets of harmonic distance. While, for nine & ten vertex (simple) graphs, we have exactly $11$ & $49$ pairs of non-isomorphic graphs (out of total $274,668$ & $12,005,168$ graphs) with the same harmonic spectra. These examples show that there are significantly very low numbers of non-unique harmonic spectrums. Moreover, we empirically found that the biharmonic distance has all unique multisets for at-least upto ten vertices ($~11$ million graphs) and we couldn’t find any non-isomorphic graphs with the same biharmonic multisets. Further, we have the following theorem regarding the uniqueness of $\mathcal{R}$.

Theorem 2 (Uniqueness of Graph Harmonic Spectrum): Let $G=(V,E,W)$ be a graph of size $\vert V\vert$ with an unweighted adjacency matrix $W$. Then, if two graphs $G_1$ and $G_2$ have the same number of nodes but different number of edges, i.e, $\vert V_1 \vert =\vert V_2 \vert$ but $\vert E_1 \vert \neq \vert E_2 \vert$, then with respect to the harmonic distance multiset, $\mathcal{R}(G_1) \neq \mathcal{R}(G_2)$.

Theorem 3 (Eigenfunction Stability of ${\rm F{\scriptsize GSD}}$): Let $\Delta \mathcal{S}_{xy}$ be the change in $\mathcal{S}_f(x,y)$ distance with respect to $\Delta w$ change in weight of any single edge on the graph. Then, $\Delta \mathcal{S}_{xy}$ for any vertex pair $(x,y)$ is bounded with respect to the function of eigenvalue as follows, $\begin{equation*} \begin{split} \Delta \mathcal{S}_{xy} & \leq 2 \big(|f(\lambda_{N-1}+2\triangle w ) -f(\lambda_{1})| \\ \end{split} \end{equation*}$

Implications: Decreasing function of $f(\lambda)$ (such as $\frac{1}{\lambda^p}$) are more stable.

Conjecture (Sparsity of ${\rm F{\scriptsize GSD}}$ Graph Spectrum): For any graph $G$, let $\big|\mathcal{R}(f(\lambda))\big|_{G}$ represents the number of unique elements present in the multiset of $\mathcal{R}$, computed on an unweighted graph $G$ based on some monotonic decreasing $f(\lambda)$ function. Then, the following holds, $\begin{equation*} \Big|\mathcal{R}(f(\lambda))\Big|_{G} \geq \Big|\mathcal{R}\Big(\frac{1}{\lambda}\Big)\Big|_{G}+2 \end{equation*}$

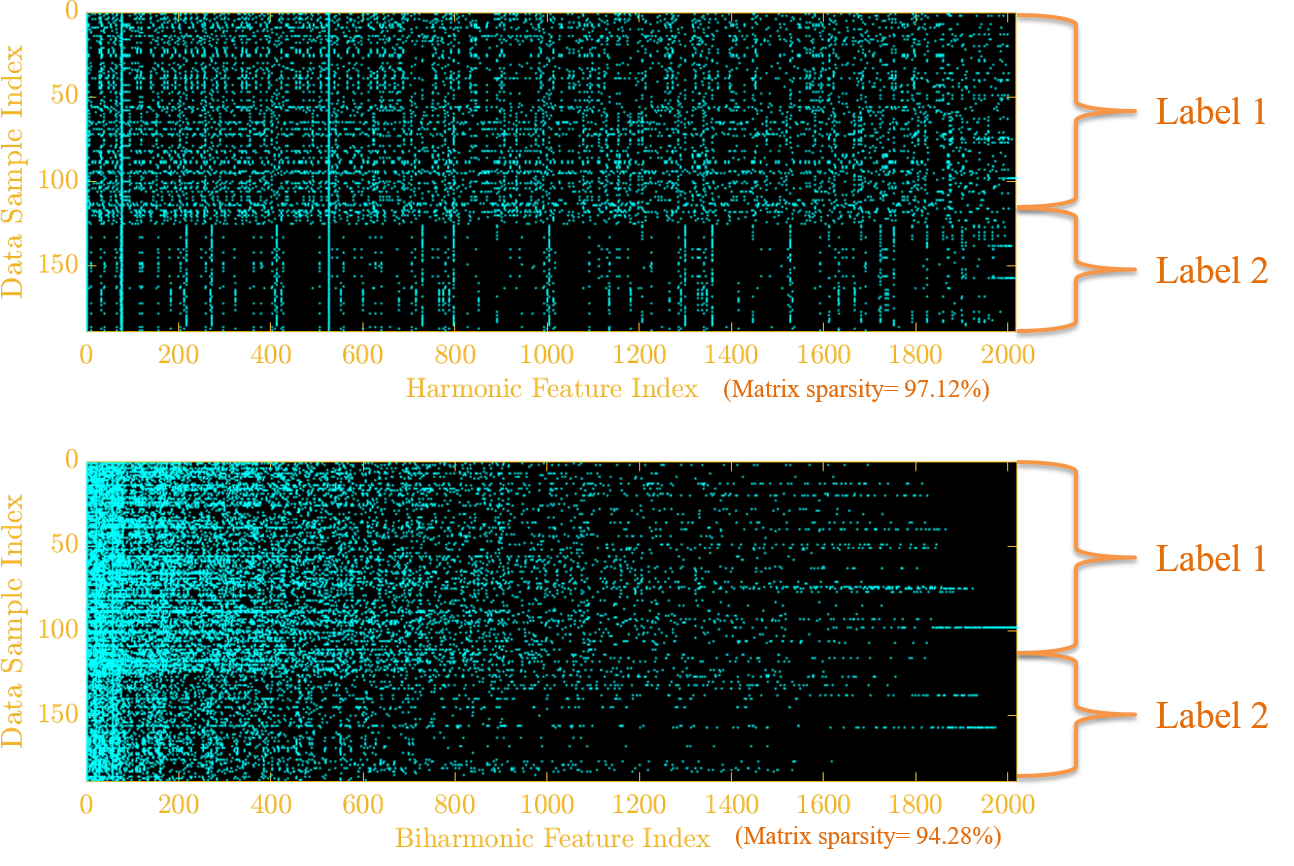
Implications: Harmonic Spectrum $(f(\frac{1}{\lambda}))$ produce the most sparse features.

Feature Space of Harmonic and Biharmonic Spectrum

Lastly, one can show that the worst case complexity of computing ${\rm F{\scriptsize GSD}}$ is $\mathcal{O}(N^2)$.

In the end, we take the histogram of ${\rm F{\scriptsize GSD}}$ spectrum to construct the graph feature vector. Overall our hunt leads to the harmonic distance as an ideal member of ${\rm F{\scriptsize GSD}}$ family for extracting graph features.

References:

1. Saurabh Verma, Zhi-Li Zhang. Hunt For The Unique, Stable, Sparse And Fast Feature Learning On Graphs. In 31st Conference on Neural Information Processing Systems (NIPS 2017). [PDF]